Filtro attivo con OpAmps
Come dimensionare un filtro con un amplificatore operazionale
Un filtro attivo è un particolare circuito che permette di isolare e permettere il passaggio solo a determinate frequenze di un segnale permettendone inoltre una modifica in termini di guadagno e di sfasamento.
Per tale scopo si utilizzano amplificatori operazionali, nelle loro configurazioni invertenti e non invertenti, sfruttando dei filtri ohmico-capacitivi.
Prima di procedere consigliamo la lettura dei seguenti articoli:
Di seguito vengono riportati schemi ed analisi delle varie configurazioni utilizzabili in base alle proprie necessità. Nel campo audio la scelta dei componenti del circuito incide in modo significativo.
Filtro attivo passa alto non invertente
Tale filtro permette il passaggio delle frequenze maggiori alla frequenza di taglio fc e permette di avere un guadagno maggiore uguale ad 1. Nel circuito sottostante si può notare la presenza di un OpAmps in configurazione non invertente alimentato tra +5V e -5V. I componenti possono essere così esaminati:
C1 – R2 → determinano la frequenza di taglio Fc e l’attenuazione in ingresso del segnale. Nel nostro caso il valore è circa 2kHz, pertanto passeranno solo le componenti di segnale a frequenza maggiore.
\(F_{c}=\frac{1}{2\cdot \pi \cdot R2 C1}\)R1 – R3 → determinano il guadagno del segnale in uscita. Il nostro segnale avrà guadagno 2.
\( \frac{ V_{out}}{V_{in} } = 1 + \frac{R1} {R3} \)Il guadagno espresso in dB è calcolabile con la relazione:

Filtro attivo passa basso non invertente
Tale filtro permette il passaggio delle frequenze minori alla frequenza di taglio fc e permette di avere un guadagno maggiore uguale ad 1.
C1 – R2 → determinano la frequenza di taglio Fc e l’attenuazione in ingresso del segnale. Nel nostro caso il valore è circa 2kHz, pertanto passeranno solo le componenti di segnale a frequenza maggiore.
\(F_{c}=\frac{1}{2\cdot \pi \cdot R2 C1}\)R1 – R3 → determinano il guadagno del segnale in uscita. Il nostro segnale avrà guadagno 2.
\( \frac{ V_{out}}{V_{in} } = 1 + \frac{R1} {R3} \)Il guadagno espresso in dB è calcolabile con la relazione:
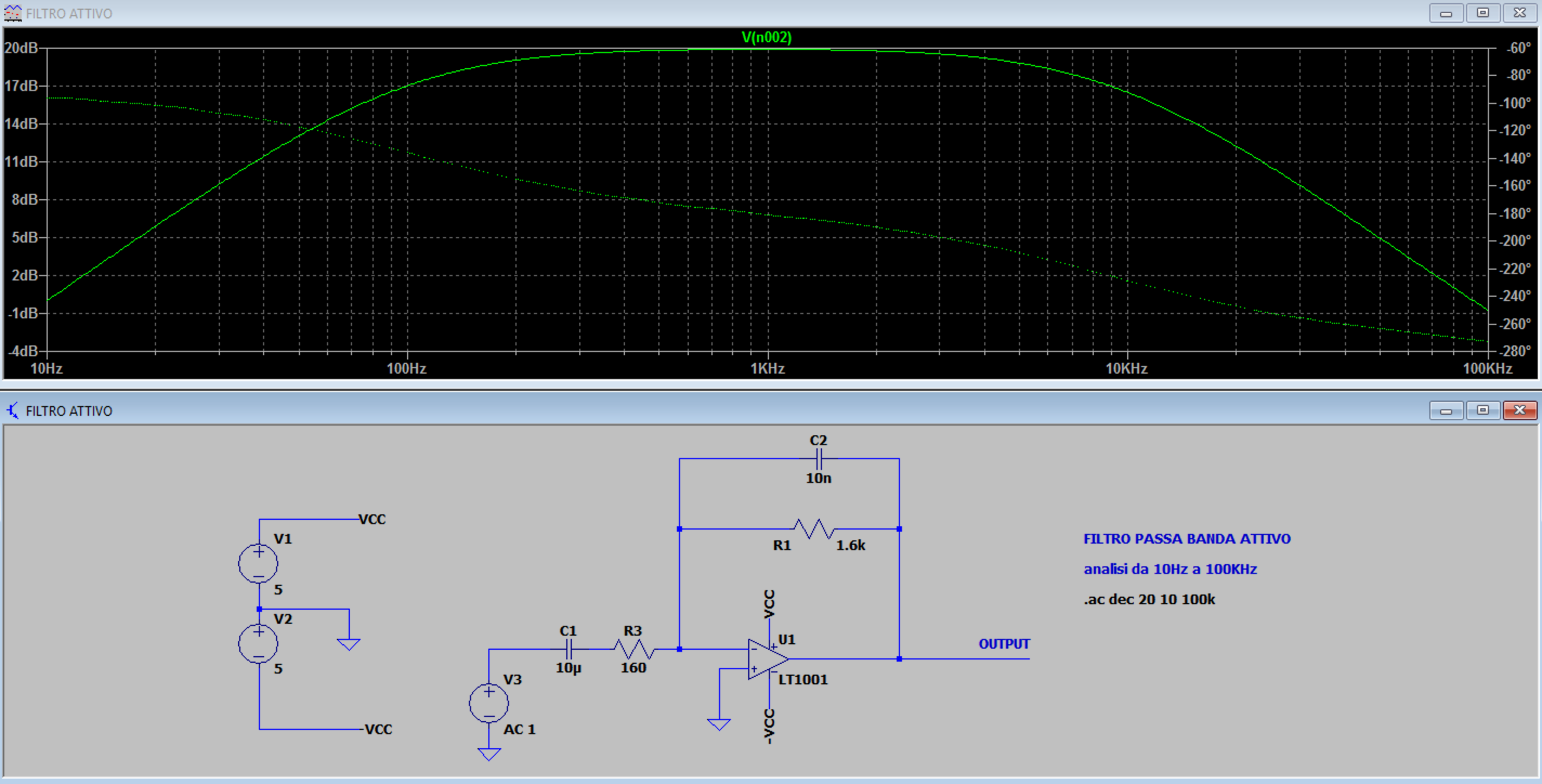
\( G_{[dB]}=20log_{10}(G) =20log_{10}(2) = 6 dB \)Filtro attivo passa banda invertente
Tale filtro permette il passaggio delle frequenze maggiori alla frequenza di taglio fc_1 e minori della frequenza di taglio fc_2 e permette di avere un guadagno maggiore uguale ad 1.
C1 – R3 → filtro passa alto con frequenza di taglio fc_1 = 100Hz
\(F_{c}=\frac{1}{2\cdot \pi \cdot R3 C1}\)C2 – R1 → filtro passa basso con frequenza di taglio fc_2 = 9,95kHz
\(F_{c}=\frac{1}{2\cdot \pi \cdot R1 C2}\)R1 – R3 → determinano il guadagno del segnale in uscita. Il nostro segnale avrà guadagno 11.
\( \frac{ V_{out}}{V_{in} } = 1 + \frac{R1} {R3} \)Il guadagno espresso in dB è calcolabile con la relazione:
\( G_{[dB]}=20log_{10}(G) =20log_{10}(11) = 20,82 dB \)