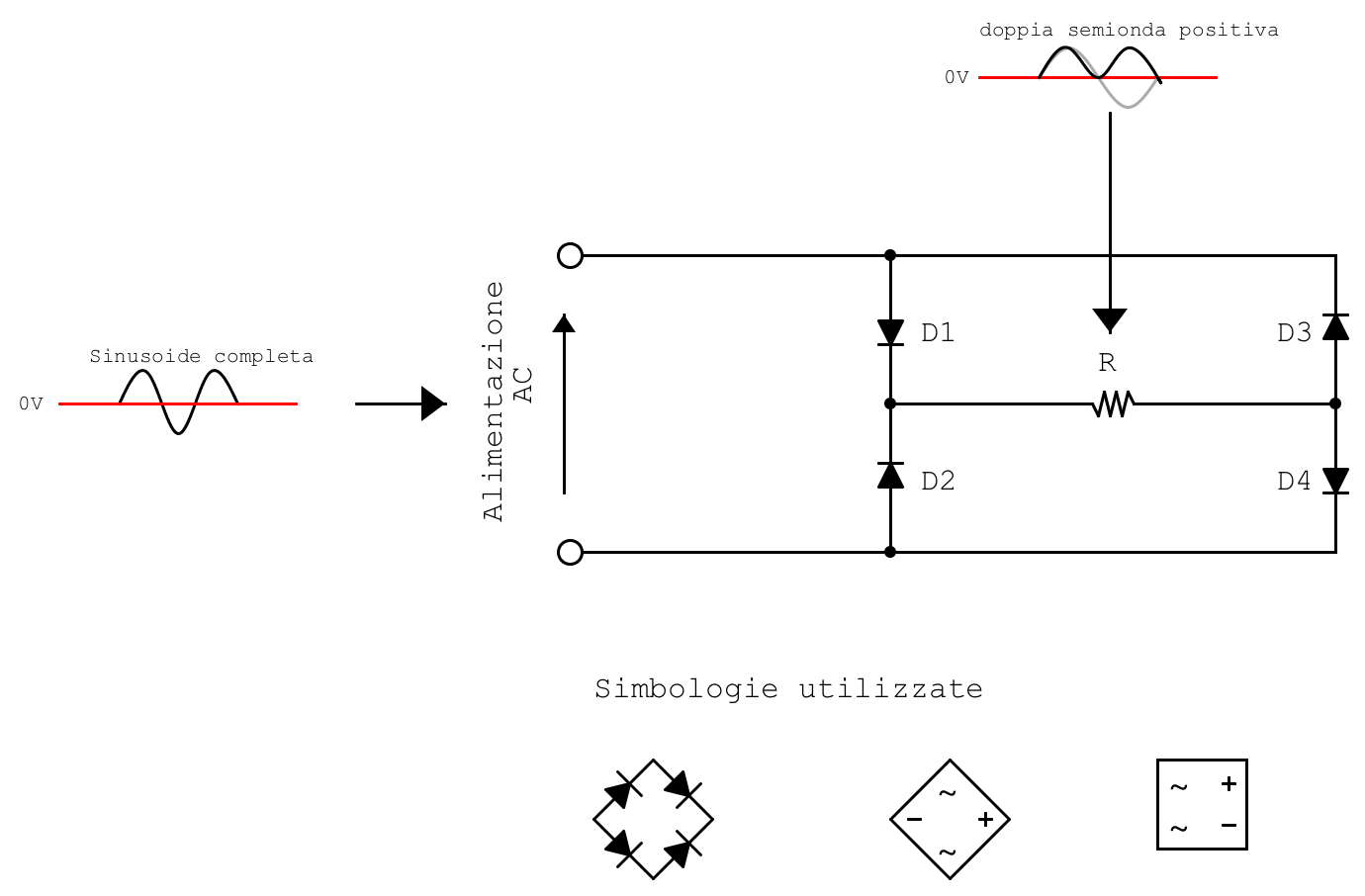
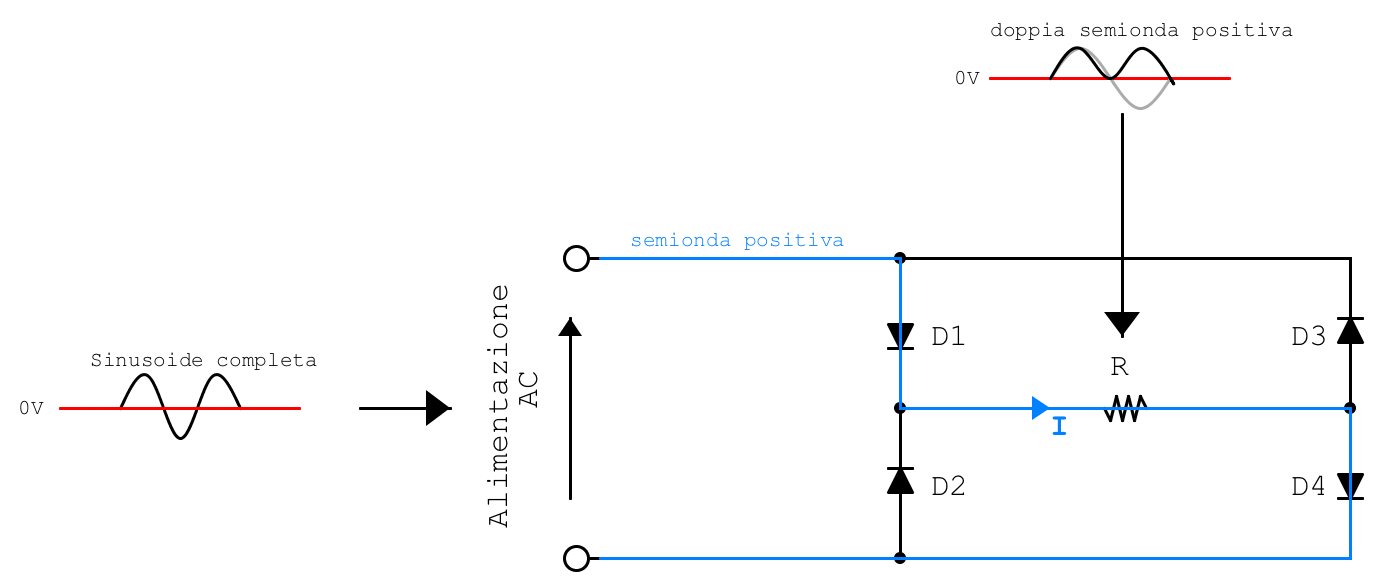
Il circuito raddrizzatore a ponte di Graetz permette di prelevare una tensione alternata AC e riportarla sul carico sotto forma di onde pulsanti positive con frequenza doppia rispetto a quella di alimentazione. Questo sistema di diodi è utilizzato nella maggior parte dei sistemi di conversione di alimentazioni da AC a DC.
Il ponte di Graetz può essere predisposto come un unico integrato avente 4 terminali o realizzato da 4 diodi a giunzione PN. La scelta tra le due tipologie viene operata in base ad esigenze tecniche di correnti in gioco, isolamento, spazio sulla PCB e fattori economici. Se si sceglie il circuito integrato si hanno 4 terminali: due di ingresso per l’alimentazione AC e due di uscitaper l’alimentazione DC (+ e -). Nel caso in cui volessimo personalizzare il ponte con diodi particolari è possibile seguire il seguente schema.
Nelle nostre prove andremo ad utilizzare dei diodi 1N4007 ed una resistenza da 100kΩ.
 Su breadboard avremo il seguente circuito:
Su breadboard avremo il seguente circuito:
 Iniziamo la nostra analisi muniti di multimetro e di oscilloscopio. Posizioniamo le sonde ai capi dell’alimentazione.
Iniziamo la nostra analisi muniti di multimetro e di oscilloscopio. Posizioniamo le sonde ai capi dell’alimentazione.
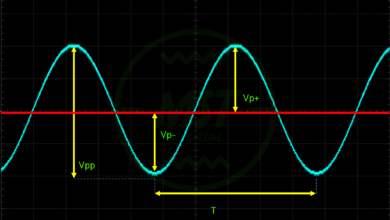
NB. nel nostro caso l’alimentazione è stata fornita da un generatore di funzioni con Vpp=10V e f=50Hz.

Essendo la frequenza di 50Hz possiamo ricavare il periodo (f=1/T) di 20ms. Avendo anche la tensione Vpp possiamo risalire alla tensione efficace misurabile con il tester impostato in tensioni AC. In questo caso la nostra Veff vale:
Il valore medio, essendo l’alimentazione alternata e periodica, è nullo. Quindi:
\(V_{medio} = 0V\)Conclusa questa prima analisi osserviamo come si comporta il circuito.
Analisi semionda positiva
Notiamo che la semionda, essendo positiva, riuscirà a percorrere la porzione di circuito evidenziata facendosi strada tra i diodi polarizzati direttamente. Ovviamente la semionda dovrà assumere un valore maggiore della tensione di soglia dei diodi. I diodi interessati dunque risultano essere D1 e D4 e la corrente percorre il mio carico nel verso indicato dalla freccia blu.
Analisi semionda negativa
Notiamo che la semionda, essendo negativa, riuscirà a percorrere la porzione di circuito evidenziata facendosi strada tra i diodi polarizzati inversamente. I diodi interessati saranno D3 e D2. Dato che la semionda in analisi è negativa, il verso della corrente sarà opposto a quello di percorrenza della nostra analisi. Ecco quindi che sul carico la corrente viene riportata con lo stesso verso dell’esempio precedente.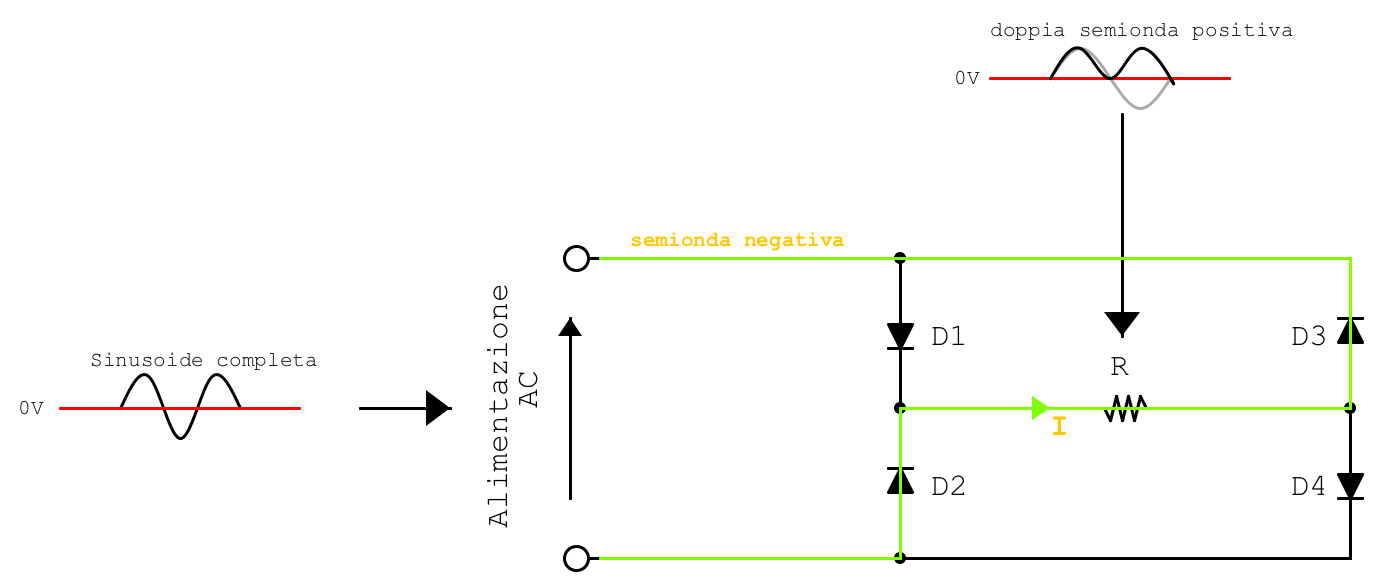
Sonda posizionata tra il diodo D3 e il diodo D4 – GND

Analisi totale
Uniamo l’analisi della forma d’onda positiva con l’analisi della semionda negativa. Otteniamo il seguente grafico:
La forma d’onda viola, come visto al paragrafo precedente, viene riportata sul carico invertita, pertanto è lecito trasformarla come segue:
Sovrapponendo il segnale bianco e il segnale viola otteniamo quindi la doppia semionda:
Infatti, sommando le forme d’onda otteniamo il seguente risultato colorato di blu:
Notiamo che sul carico si ha un susseguirsi di semionde positive grazie al gioco di polarizzazioni creato dai di diodi. Pertanto, sempre sul carico, si ha un’onda pulsante al doppio della frequenza poiché il periodo sarà dimezzato.
Come per il raddrizzatore a singola semionda, anche con il ponte di Graetz abbiamo un piccolo tempo t per il quale il nostro carico non è alimentato. Questo fenomeno è dovuto dal fatto che la tensione di alimentazione, in quel tempo t è minore della tensione di soglia del diodo. Per superare tale problema possiamo ricorrere ai condensatori di livellamento da porre in parallelo al carico.
Sull’onda raddrizzata e non livellata possiamo procedere con l’analisi matematica (informazioni prelevate da penultima immagine):
\(V_{eff} = \frac{Vp}{\sqrt{2}} = \frac{5.36}{\sqrt{2}} = 3.79V\)Il valore medio, non essendo l’alimentazione più alternata, non è nullo. Quindi:
\(V_{medio} = \frac{2 \cdot Vp}{\sqrt{\pi}} = \frac{2 \cdot 5.36}{\sqrt{\pi}} = 3.14V\)Come per il raddrizzatore a singola semionda, detto anche half-wave bridge, possiamo procedere con il calcolo del fattore di forma e del ripple. Il fattore di fattore forma, viene indicato con Kf e rappresenta il rapporto tra valore efficace della tensione e il valore medio del segnale stesso. Se l’alimentazione è a singola semionda, il carico è puramente resistivo e non vi è alcun condensatore di livellamento applicato, avremo:
\(K_{f}=\frac{V_{efficace}}{V_{medio}} = \frac{\frac{Vp}{\sqrt{2}}} {\frac{2 \cdot Vp}{{\pi}}} = \frac{\pi}{2\sqrt{2}}= 1.11\)Da questo dato di partenza possiamo risalire al nostro coefficiente di ripple r definito come:
\(r=\sqrt{K_{f}^{2}-1} = \sqrt{1.11^{2}-1} = 0.48\)LIVELLAMENTO
Concludiamo la nostra analisi introduttiva sul ponte di Graetz studiando la sua reazione al livellamento. Per livellare la doppia semionda sarà necessario inserire in parallelo al carico un condensatore, al fine di sfruttarne la continua carica/scarica. Ovviamente condensatori di piccola taglia svolgeranno un cattivo livellamento.
C=10nF R=100K f=50Hz Vmedia=1.33V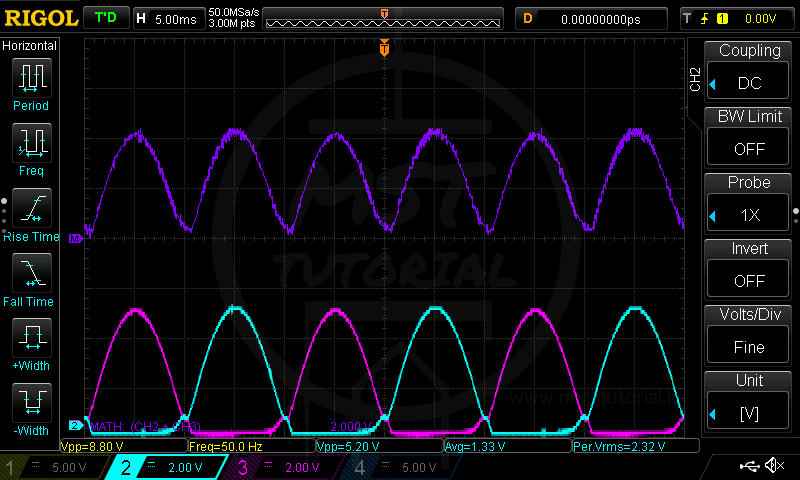 Livellamento molto scadente, il carico è alimentato in modo pulsante con variazioni di tensione di 5.20V.
Livellamento molto scadente, il carico è alimentato in modo pulsante con variazioni di tensione di 5.20V.
C=100nF R=100K f=50Hz Vmedia=1.72V
 Livellamento scadente, il carico è alimentato in modo pulsante con variazioni di tensione di circa 2V.
Livellamento scadente, il carico è alimentato in modo pulsante con variazioni di tensione di circa 2V.

 Notiamo la tensione Vp azzurra è minore della Vp gialla. Questo è dovuto alla caduta di tensione sul diodo.
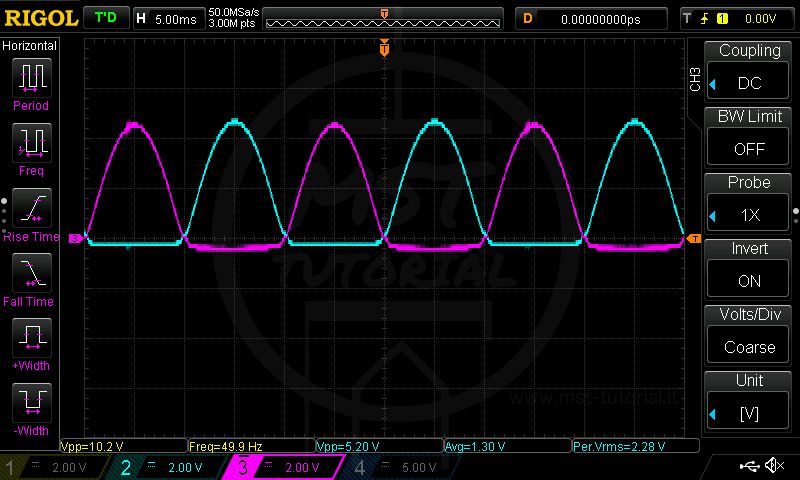
Notiamo la tensione Vp azzurra è minore della Vp gialla. Questo è dovuto alla caduta di tensione sul diodo.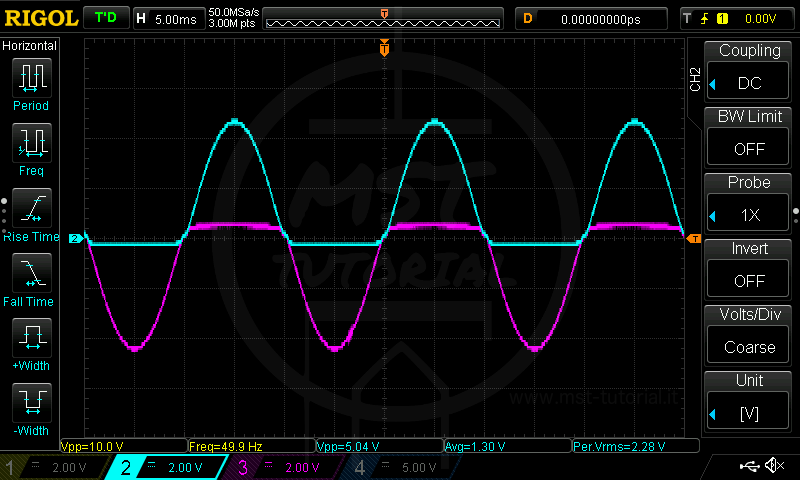


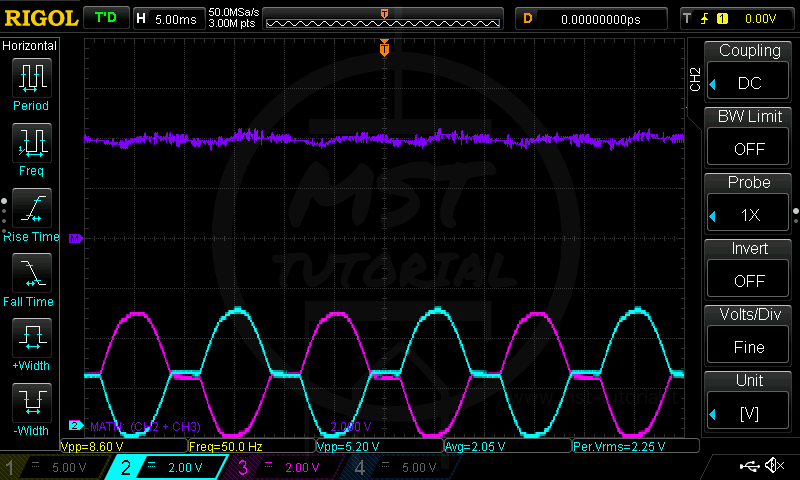 Livellamento accettabile, il carico è alimentato ma con variazioni di tensioni di 0.3V.
Livellamento accettabile, il carico è alimentato ma con variazioni di tensioni di 0.3V. Livellamento buono, il carico è alimentato con costanza con fluttuazioni di tensione minori di 0.1V.
Livellamento buono, il carico è alimentato con costanza con fluttuazioni di tensione minori di 0.1V.