Metodo Kirchhoff: risoluzione reti lineari AC e DC

Gustav Robert Georg Kirchhoff (1824 – 1887) è stato un fisico e matematico tedesco che, nel 1845, formulò le due leggi dei circuiti a parametri concentrati, che sono una conseguenza dei principi di conservazione della carica e dell’energia.

Nello specifico formulò due leggi che, ad oggi, sono alla base tutti i modelli matematici utilizzati sia nei circuiti lineari alimentati in DC sia nei circuiti lineari alimentati in AC. Tali leggi infatti presero il nome di:

• KCL (Kirchhoff’s Current Law), in italiano detta anche legge ai nodi, detta prima legge di Kirchhoff.
• KVL (Kirchhoff’s Voltage Law), in italiano detta anche legge alle maglie, detta seconda legge di Kirchhoff.

Definizioni: nodo, ramo e maglia

Prima di procedere quindi è doveroso fare una breve descrizione di un circuito elettrico e delle parti che lo compongono.

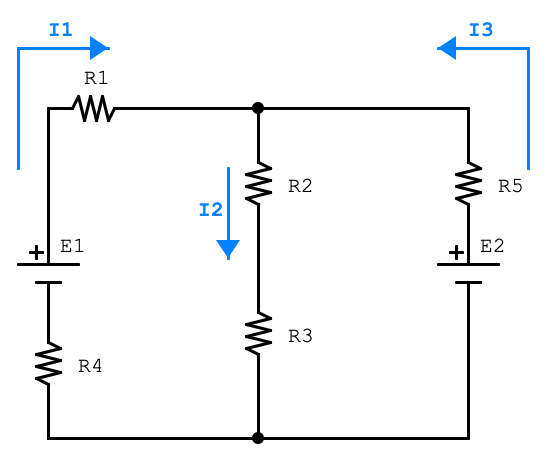
Prendendo in esame il circuito proposto, composto da cinque resistori e due generatori di tensione, possiamo definire:

Un nodo elettrico è un punto specifico (nella realtà un morsetto o una connessione di derivazione) nella quale si uniscono tra loro più estremità di rami diversi. In questo punto ci sono correnti entranti e correnti uscenti. Nello schema proposto si possono individuare due nodi elettrici.

Esempio di nodi elettrici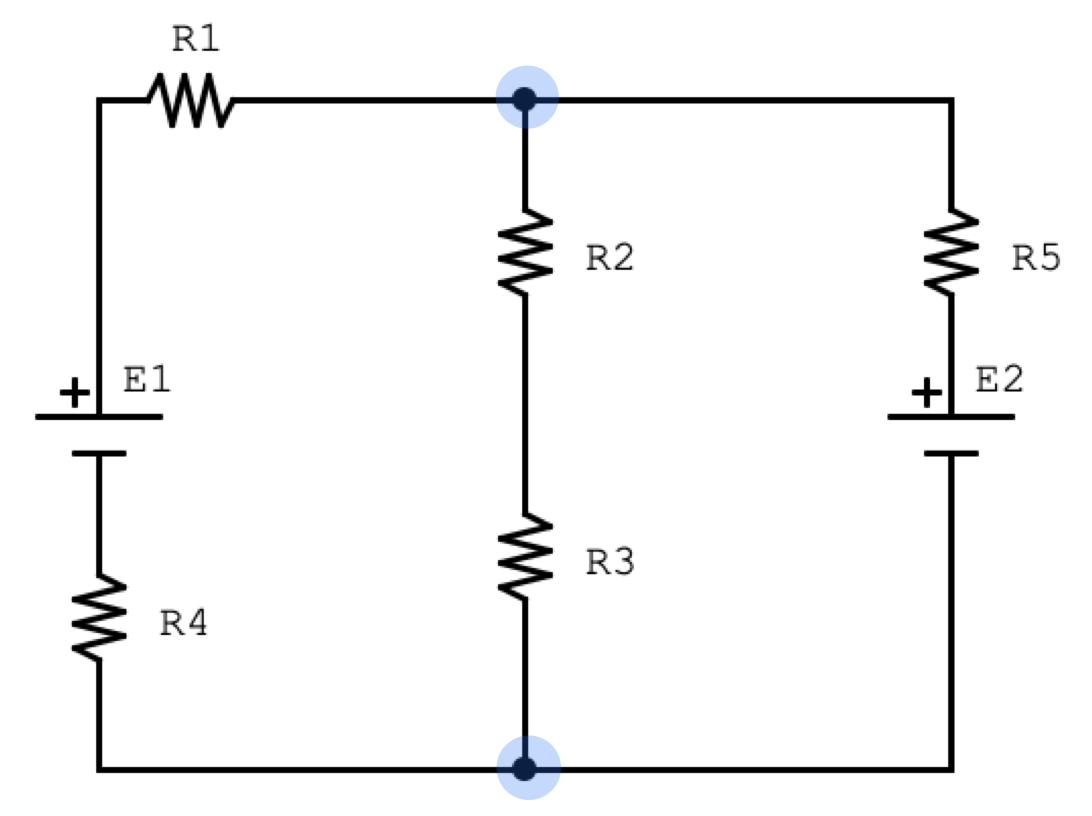: sono presenti 2 nodi

Un ramo elettrico coincide con una tratta di cavo e componenti in serie tra loro racchiusi tra due nodi. Si può intendere ramo anche ogni singola tratta attraversata dalla medesima corrente elettrica e contenuta tra due nodi.

Esempio di rami elettrici: sono presenti tre rami

Una maglia elettrica è un anello chiuso all’interno di un circuito (che include quindi più rami).

Esempio di maglie elettriche: sono presenti 3 maglie.

Prima legge di Kirchhoff (KCL): legge ai nodi

Come anticipato, la prima legge di Kirchhoff riguarda l’analisi dei nodi. Essi possono esser interpretati come un vero e proprio incrocio stradale dove vi sono correnti che arrivano e correnti che se ne vanno, o meglio, correnti entranti nel nodo e correnti uscenti dal nodo. La legge KCL, per quanto banale e ovvia possa essere, è alla base di ogni studio elettrotecnico:

La somma delle correnti entranti in un nodo coincide con la somma delle correnti uscenti

oppure

La somma tra tutte le correnti entranti (indicate con segno positivo per convenzione) e tutte le correnti uscenti (indicate con segno negativo per convenzione) deve risultare 0.

Quindi a livello matematico possiamo esprimere

\( \sum_{k} I_{k(ENTRANTI)} = \sum_{j} I_{j(USCENTI)}\)

oppure

\( \sum_{k} I_{k(ENTRANTI)} – \sum_{j} I_{j(USCENTI)} = 0\)

In forma compatta la KCL si scrive come somma algebrica di tutte le correnti del nodo, ciascuna con il proprio segno: \(\sum_{k} I_{k} = 0\).

Prendendo in esame quindi il nostro circuito possiamo dichiarare quindi che:

nodo superiore     I1 + I3 = I2
nodo inferiore       I2 = I1 + I3

L’equazione del nodo inferiore coincide con quella del nodo superiore: per questo, in un circuito con n nodi, le equazioni ai nodi indipendenti sono solo n − 1 (qui 2 − 1 = 1).

Seconda legge di Kirchhoff (KVL): legge alle maglie

La seconda legge di Kirchhoff KVL, invece, riguarda l’analisi delle maglie. Esse, come già detto, possono esser individuate da un anello (percorso) chiuso all’interno del circuito coinvolgendo di fatto due o più rami. Si vanno ad osservare le tensioni e si dovrà rispettare la seguente regola:

La sommatoria delle tensioni concordi dovrà esser uguale alla sommatoria delle cadute di tensioni (tensioni discordi).

oppure

La sommatoria tra le tensioni concordi (indicate con segno positivo) e la sommatoria delle tensioni discordi (indicate con segno negativo) deve risultare 0

Per applicare la regola si fissa prima un verso di percorrenza della maglia (ad esempio orario): una tensione è concorde se è orientata nello stesso verso di percorrenza, discorde se è orientata in verso opposto. Il verso scelto è arbitrario: invertendolo cambiano tutti i segni, ma l’equazione resta la stessa.
Quindi a livello matematico possiamo esprimere

\( \sum_{k} V_{k(concordi)} = \sum_{j} V_{j(discordi)}\)

oppure

\( \sum_{k} V_{k(concordi)} – \sum_{j} V_{j(discordi)} = 0\)

 

L’errore tipico da evitare è la gestione dei versi delle tensioni: tipicamente si indica in senso orario il verso di tensione (e di corrente uscente) del primo generatore e di conseguenza gli altri sarà facile individuarli. I carichi avranno caduta di tensione opposta al verso della corrente e i versi di eventuali altri generatori di tensione o corrente saranno indicati dalle corrispettive polarità.

M1 –>     E1 – R1I1 – R2I2 – R3I2 – R4I1 = 0
M2 –>     R3I2 + R2I2 + R5I3 – E2 = 0
M3 –>    E1 – R1I1 + R5I3 – E2 – R4I1 = 0

Metodo di risoluzione e numero di equazioni

Prima di procedere domandiamoci: perché utilizzare il metodo di risoluzione Kirchhoff? Molto semplicemente vi sono alcuni casi in cui, dati molti generatori, dati carichi connessi in particolare modo, non è possibile risolverli con le relazioni base del mondo elettrotecnico. Ecco quindi che viene in soccorso non una formula ma un vero modello matematico da seguire.

Ora, avendo tutto il materiale per procedere al metodo di risoluzione matematico, si può apprendere il numero di equazioni delle quali si ha bisogno per risolvere un certo circuito.

• ( n – 1 ) equazioni ai nodi (dove n rappresenta il numero di nodi presenti nel circuito).
• l – ( n – 1 ) equazioni alle maglie (dove l rappresenta il numero di rami elettrici).

Le equazioni si possono scrivere in modo arbitrario purché siano indipendenti tra loro: per i nodi basta escluderne uno qualsiasi, mentre le maglie scelte devono essere indipendenti, cioè ognuna deve contenere almeno un ramo non utilizzato dalle maglie precedenti. In una rete planare una scelta sempre valida è quella delle maglie elementari (le “finestre” del circuito, che non contengono altri rami al loro interno); in alternativa si usa il metodo dell’albero e del coalbero. Non è invece necessario che ogni maglia contenga un generatore.

Tornando al nostro esempio quindi sarà necessaria una equazione ai nodi e due equazioni alle maglie (nell’esempio sotto riportato si sono scelte M1 e M2; la maglia M3 non è indipendente, perché la sua equazione si ottiene sommando membro a membro le equazioni di M1 e M2: i termini R₂I₂ e R₃I₂ si elidono e resta E₁ − R₁I₁ − R₄I₁ + R₅I₃ − E₂ = 0, cioè proprio M3).

\( \left\{\begin{matrix}
I_{1} + I_{3} = I_{2}\\
E_{1} – R_{1}I_{1} – R_{2}I_{2} – R_{3}I_{2} – R_{4}I_{1}= 0 \\
R_{3}I_{2} + R_{2}I_{2} + R_{5}I_{3} – E_{2} = 0\\
\end{matrix}\right.
\)

Esempio svolto in DC

A questo punto si può procedere alla risoluzione matematica. Assegniamo, a titolo di esercizio, i seguenti valori (con i versi delle correnti indicati in figura): E₁ = 20 V, E₂ = 10 V, R₁ = R₄ = 2 kΩ, R₂ = R₃ = 1 kΩ, R₅ = 2 kΩ. Esprimendo le resistenze in kΩ le correnti risultano in mA, e il sistema diventa:

\( \left\{\begin{matrix}
I_{2} = I_{1} + I_{3}\\
20 – 4\,I_{1} – 2\,I_{2} = 0 \\
2\,I_{2} + 2\,I_{3} – 10 = 0\\
\end{matrix}\right.
\)

Sostituendo la prima equazione nelle altre due si ottiene:

\( \left\{\begin{matrix}
3\,I_{1} + I_{3} = 10\\
I_{1} + 2\,I_{3} = 5\\
\end{matrix}\right.
\)

Dalla seconda ricaviamo I₁ = 5 − 2·I₃ e, sostituendo nella prima, 15 − 5·I₃ = 10, quindi:

\(I_{3} = 1\,mA \qquad I_{1} = 3\,mA \qquad I_{2} = I_{1} + I_{3} = 4\,mA\)

Tutte le correnti risultano positive, quindi i versi scelti in figura coincidono con quelli reali (una corrente negativa indicherebbe semplicemente un verso reale opposto a quello ipotizzato).

Verifica con la maglia M3: E₁ − R₁I₁ + R₅I₃ − E₂ − R₄I₁ = 20 − 6 + 2 − 10 − 6 = 0 V.

Verifica con il bilancio delle potenze: i generatori erogano P = E₁I₁ + E₂I₃ = 20·3 + 10·1 = 70 mW, mentre i resistori dissipano R₁I₁² + R₄I₁² + R₂I₂² + R₃I₂² + R₅I₃² = 18 + 18 + 16 + 16 + 2 = 70 mW. Potenza generata e dissipata coincidono, quindi la soluzione è corretta.

Reti con generatori di corrente

N.B. Può capitare che all’interno del circuito elettrico siano presenti anche dei generatori di corrente. In tal caso il numero di equazioni necessarie alla risoluzione cambia. Infatti si avrà la necessità di:

• ( n – 1 ) equazioni ai nodi (dove n rappresenta il numero di nodi presenti nel circuito).
• l – p – ( n – 1 ) equazioni alle maglie (dove l rappresenta il numero di rami elettrici e p il numero di rami che possiedono generatori di corrente).

Ad esempio il seguente circuito necessita di 4 equazioni totali:

\( \left (n-1 \right ) = \left (2-1 \right ) = 1 eq.nodi
\) \( l – p – \left (n-1 \right ) = 5 – 1 – 1 = 3 eq.maglie
\)

Reti in corrente alternata

Le leggi di Kirchhoff valgono anche nei circuiti lineari alimentati in AC, in regime sinusoidale. In questo caso tensioni e correnti si rappresentano con i fasori (numeri complessi che ne indicano valore efficace e fase) e i componenti con le rispettive impedenze: Z = R per i resistori, Z = jωL per gli induttori e Z = 1/(jωC) = −j/(ωC) per i condensatori. KCL e KVL diventano somme algebriche di fasori:

\(\sum_{k} \bar{I}_{k} = 0 \qquad \sum_{k} \bar{V}_{k} = 0\)

e il procedimento (scelta di n − 1 nodi e di l − (n − 1) maglie indipendenti, scrittura e risoluzione del sistema) resta identico a quello visto in DC, con la sola differenza che i calcoli si eseguono con numeri complessi. Per le grandezze alternate vedi Alimentazione AC – Alternating Current; per le reattanze di condensatori e induttori vedi Condensatori e Induttori.

Articoli collegati

• Metodo Millman: risoluzione reti lineari (metodo più rapido per le reti a due nodi)
• Resistore: resistenza elettrica e resistività elettrica
• Alimentazione AC – Alternating Current