Il circuito raddrizzatore a singola semionda consiste in una tecnica dove si preleva una tensione alternata AC e si riportano al carico solo le semionde positive o solo le semionde negative. La realizzazione di tale circuito è banalissima e richiede pochi componenti:
- Alimentazione AC (da trasformatore o da generatore di funzioni)
- 1 diodo in silicio a giunzione PN (nel nostro caso utilizzeremo un 1N4007)
- 1 carico da alimentare in DC (nel nostro caso un resistore da 100k)
- 1 condensatore di livellamento (valore da calcolare)
Conoscenze base per poter procedere:
 |
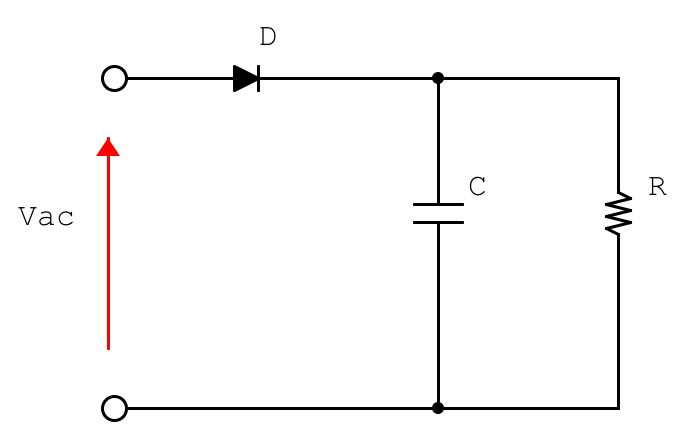
Per prima cosa osserviamo lo schema elettrico: notiamo una alimentazione Vac alternata ad una certa frequenza f. Essa, prima di giungere al carico R passa per un diodo D e un condensatore C. Giunti a questo punto è d’obbligo fare due richiami teorici.
- Il diodo è un componente passivo non lineare che permette il passaggio di corrente in un solo verso. Pertanto, se alimentato da una alimentazione alternata, superata la tensione di soglia, permetterà il passaggio di solo semionde positive (se polarizzato direttamente) o di sole semionde negative (se polarizzato inversamente). Nel nostro caso è chiaramente polarizzato direttamente, pertanto al carico giungono solo le semionde positive.
- Il condensatore è un componente in grado di immagazzinare cariche elettriche per poi rilasciarle in un secondo momento. Sfrutteremo quindi il fenomeno della carica/scarica di un condensatore al fine di livellare (rendere il più possibile continua) la tensione sul carico.
NB. è necessario prestare attenzione alla polarità dei condensatori elettrolitici.
 Su breadboard ci ritroveremo un circuito simile al seguente:
Su breadboard ci ritroveremo un circuito simile al seguente: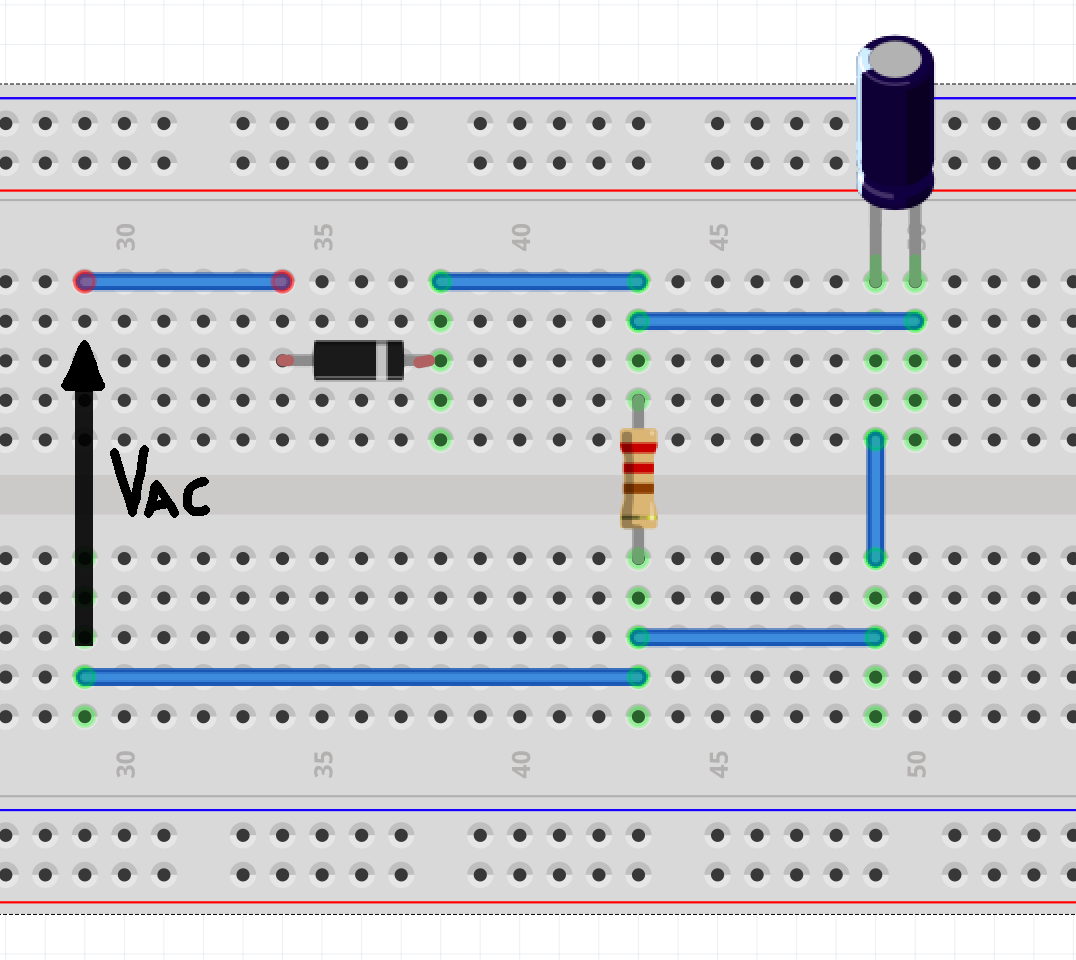 Definiamo le seguenti grandezze valide solo per la configurazione a singola semionda:
Definiamo le seguenti grandezze valide solo per la configurazione a singola semionda:
- Valore medio della tensione di uscita a vuoto
\(V_{odc} = \frac{V_{alimentazioneMAX}}{\pi}\) - Corrente massima nel diodo
\(I_{FM} = \frac{V_{alimentazioneMAX}}{R_{carico}}\) - Corrente media nel diodo
\(I_{F(av)} = \frac{V_{alimentazioneMAX}}{\pi \cdot R_{carico}}\) - Tensione massima inversa su diodo
\(V_{RRM} = V_{alimentazioneMAX}\)
In un primo momento rimuoviamo il condensatore in modo tale da osservare il fenomeno primario dovuto dal diodo D. Per la prova è stato utilizzato un resistore da 220kΩ, nessun condensatore C e un diodo 1N4007. L’alimentazione è stata fornita da un generatore di funzioni con una Vpp di 8.9V e una frequenza di 50Hz.
Collegando una sonda dell’oscilloscopio sull’alimentazione (segnale giallo) e una sul carico (segnale azzurro) si ottiene quanto segue:
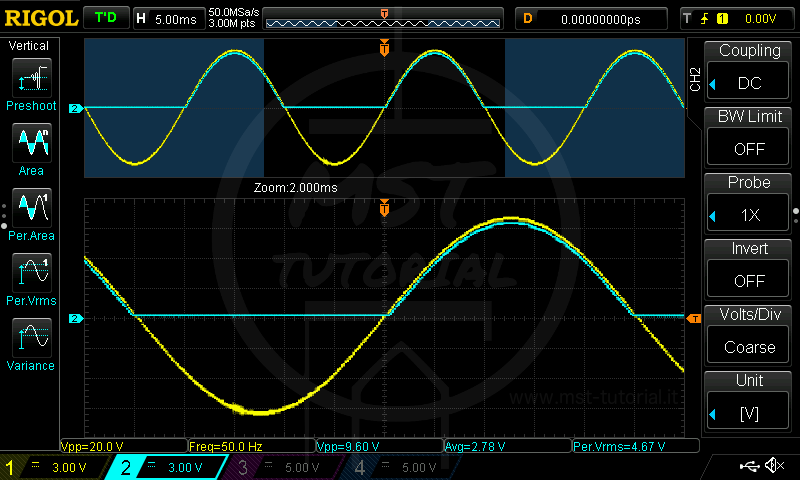
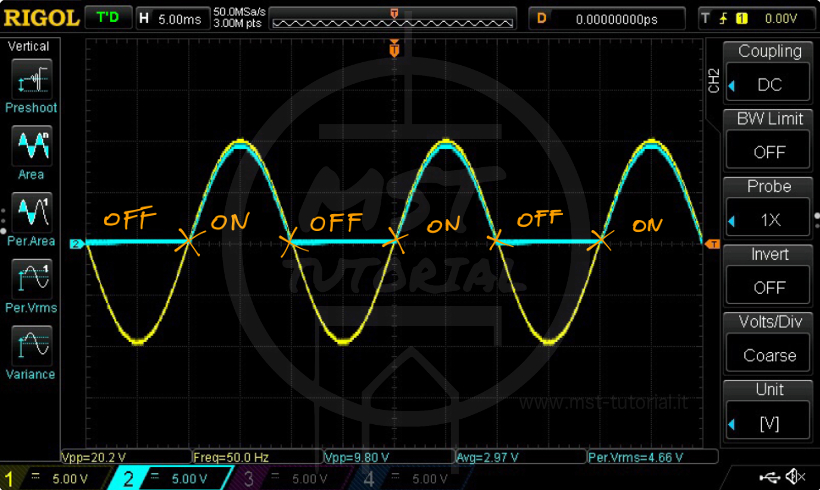
Notiamo che sul carico giunge solo la semionda positiva con una tensione di picco positiva minore rispetto l’alimentazione. Questo fenomeno è dovuto alla caduta di tensione sul diodo stesso.
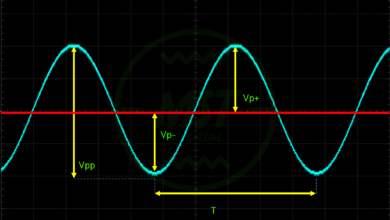
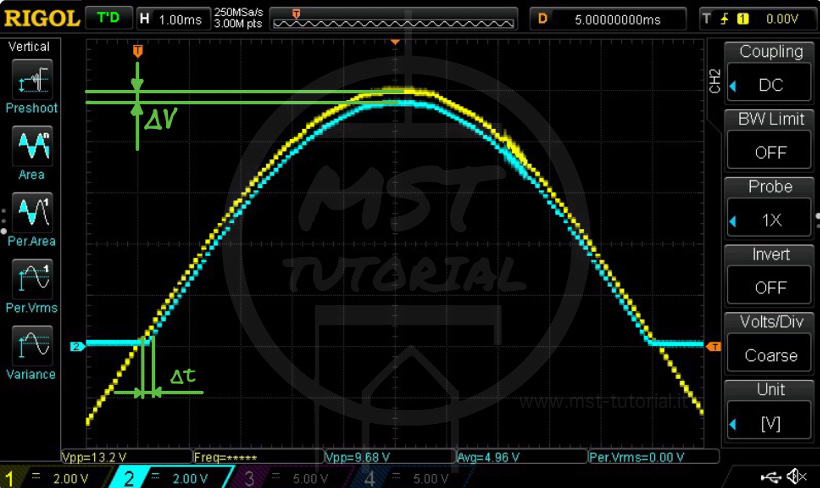 Notiamo come vi sia una caduta di 0.3 divisioni e quindi, considerando che \(\frac{Volts}{div} = 2V\) otteniamo una caduta di tensione ΔV di circa:
Notiamo come vi sia una caduta di 0.3 divisioni e quindi, considerando che \(\frac{Volts}{div} = 2V\) otteniamo una caduta di tensione ΔV di circa:
Notiamo anche come il diodo non entri in conduzione subito, ma solo al raggiungimento della tensione di soglia. Viene così a nascere un ritardo Δt. Considerando che nell’immagine sopra riportata l’oscilloscopio era impostato in \(\frac{Time}{div} = 1ms\) possiamo calcolare:
\(\Delta t = n div \cdot \frac{Time}{div} = 0.3 \cdot 1 = 0.3ms\)Infine, si può facilmente notare anche come il nostro carico non sia alimentato per un tempo pari a circa metà periodo. Pertanto è possibile affermare che questa tipologia di alimentazione è totalmente inadatta a carichi sensibili, poiché verrebbero alimentati in modo non continuativo e con una tensione variabile tra 0V e Vp+.
Partendo dall’ultima figura, ottenuta con \(\frac{Volts}{div} = 5V\) e \(\frac{Time}{div} = 5ms\), possiamo iniziare l’analisi matematica. La tensione di alimentazione è di 20.2V di picco-picco. Essendo la tensione sinusoidale alternata possiamo calcolare il valore efficace:
\(V_{efficace} = \frac{Vp+}{\sqrt{2}} = \frac{10.1}{\sqrt{2}} = 7.14V\)Il valore medio di alimentazione, per definizione di segnale alternato, sarà nullo:
\(V_{m} = 0V\)Ora analizziamo la tensione raddrizzata sul carico. Senza alcun condensatore di livellamento applicato possiamo calcolare la tensione efficace:
\(V_{efficace} = \frac{Vp+}{2} = \frac{9.8}{2} = 4.9V\)e la tensione media:
\(V_{m} = \frac{Vp+}{{\pi}} = \frac{9.8}{{\pi}} =3.11V\)A questo punto possiamo connettere il nostro condensatore. In base alla capacità scelta/calcolata avremo un determinato livellamento. Condensatori con piccole capacità si scaricheranno prima portando ad un livellamento peggiore rispetto a condensatori con capacità maggiori. Man mano che il livellamento migliora avremo un abbassamento della Vpp ed un aumento della componente continua. In altre parole avremo un abbassamento della tensione efficace ed un aumento della tensione media.
Osserviamo i diversi livellamenti aggiungendo nel nostro circuito condensatori di taglia diversa.
C=100nF D=1N4007 R=100K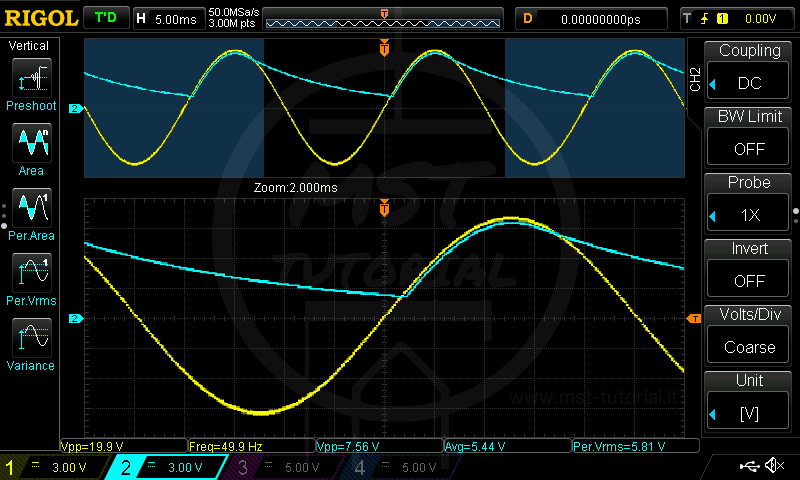 La capacità risulta sufficiente per un cattivo livellamento. Il nostro carico non sarà mai disalimentato ma sarà sottoposto a continue fluttuazioni di tensione di circa 6V di picco-picco.
La capacità risulta sufficiente per un cattivo livellamento. Il nostro carico non sarà mai disalimentato ma sarà sottoposto a continue fluttuazioni di tensione di circa 6V di picco-picco.
C=1000nF D=1N4007 R=100K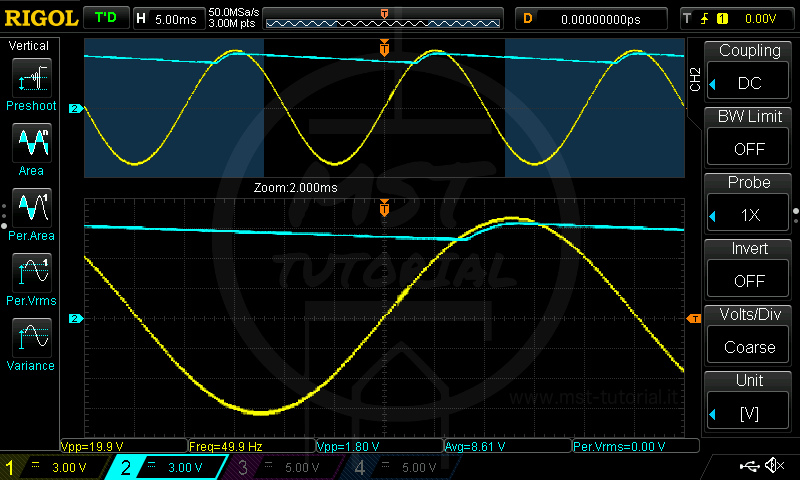 La capacità permette un livellamento mediocre. Il carico è sottoposto a continue fluttuazioni di tensione di circa 1.8V di picco-picco.
La capacità permette un livellamento mediocre. Il carico è sottoposto a continue fluttuazioni di tensione di circa 1.8V di picco-picco.
C1 = 10000nF D=1N4007 R=100K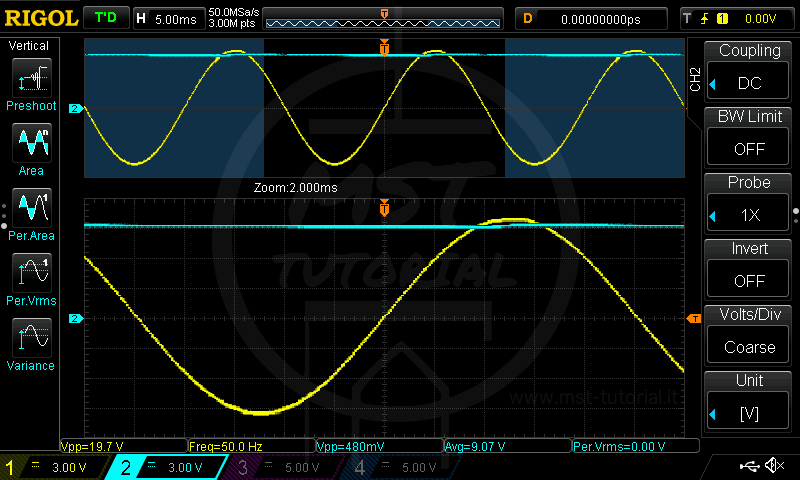 La capacità permette un buon livellamento. Il carico è comunque sottoposto a continue fluttuazioni di tensione di circa 0.48V di picco-picco.
La capacità permette un buon livellamento. Il carico è comunque sottoposto a continue fluttuazioni di tensione di circa 0.48V di picco-picco.
Infine, osservati questi grafici introduciamo ora le ultime grandezze elettriche di nostro interesse: il ripple e il fattore forma.
Il fattore di fattore forma, viene indicato con Kf e rappresenta il rapporto tra valore efficace della tensione e il valore medio del segnale stesso. Se l’alimentazione è a singola semionda, il carico è puramente resistivo e non vi è alcun condensatore di livellamento applicato, avremo:
\(K_{f}=\frac{V_{efficace}}{V_{medio}} = \frac{\frac{Vp+}{2}}{\frac{Vp+}{{\pi}}} = \frac{\pi}{2}= 1.57\)Da questo dato di partenza possiamo risalire al nostro coefficiente di ripple r definito come:
\(r=\sqrt{K_{f}^{2}-1} = \sqrt{1.57^{2}-1} = 1.21\)Inserendo in parallelo al carico un condensatore, si avrà una riduzione del valore efficace ed un incremento del valore medio. Di conseguenza si avrà un coefficiente Kf minore che comporterà a sua volta una riduzione del ripple. Più quest’ultimo sarà ridotto e tendente allo zero, e migliore sarà il nostro raddrizzatore a singola semionda.


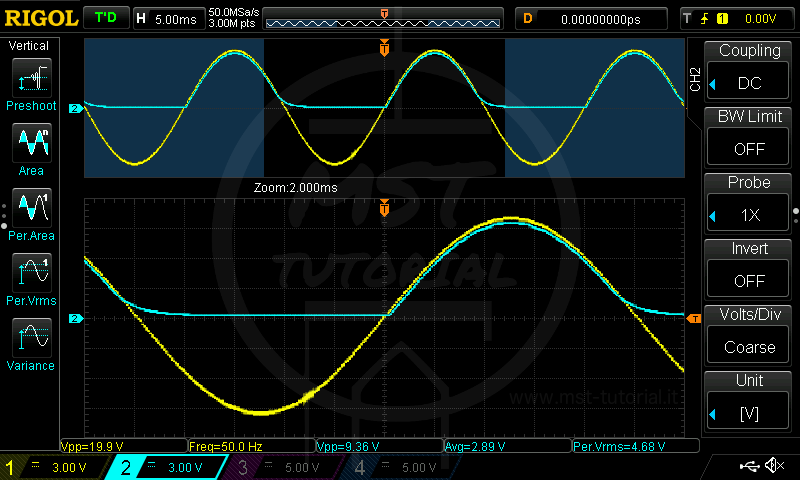 Il livellamento è debolissimo, il nostro carico risulta non essere alimentato per quasi metà periodo.
Il livellamento è debolissimo, il nostro carico risulta non essere alimentato per quasi metà periodo.